Unfug auf der Kommandozeile

David G. Wiseman» hat auf seiner Seite eine Liste lustiger Kommandozeilenkommandos» hinterlassen. Mein Favorit ist hierbei

% %blow
%blow: No such job.

Ahem.

Von Text zu Text

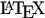So ergab es sich am heutigen Tage, dass nach einiger Zeit der Probierens, es (ja was denn eigentlich?) mir nun endgültig gelang, ein mehr oder minder komplexes Dokument in in ein mehr oder minder anderes komplexes Dokument in HTML zu konvertieren. Schier unendlich hohe Hürden mussten gemeistert werden, ehe das Dokument so stand, wie es nun steht.

Doch immer langsam mitte Pferde. Eigentlich dachten wir (Clemens» und ich), dass es doch eine tolle Sache wäre, wenn man die Dokumentation für ein Softwareprodukt» doch gerne nur einmal schreibt, gerade so, dass man sie auch ausdrucken kann, und dass man dann eine Version für die Veröffentlichung im Internet automatisch generieren lässt. Soweit so gut. Recht schnell war dann auch schließlich das 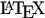-Dokument fertig gestellt. Also *zack* wacker zu einem frickelig zusammengehackten Stück Software in Perl gegriffen (auch bekannt unter dem vielversprechenden Namen latex2html»). Irgendwie wollte das jedoch überhaupt nicht hinhauen. Nach einer kleinen Suche, tauchte dann noch ein kleines anderes Stück Software mit Namen tex2page» auf. In Scheme geschrieben, schnell installiert und es macht genau das, was man von ihm verlangt.

Danke für diese Eingebung. Ich werde niemals nie nimmer wieder auf frickelige Perl-Software ausweichen und stets dem λ-kalkülisierten Scheme treu bleiben. In tiefer Verbeugung und mit ewiger Dankbarkeit dem Entwickler von tex2page».

Wer die Ergebnisse einmal vergleichen möchte, findet unten die beiden Links, die jeweils einmal auf das ursprüngliche PDF, das aus dem 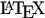-Dokument erzeugt wurde, sowie die automatisch generierte HTML-Version davon verweisen.

• PDF»
• HTML»

Funktionen und Mengen

Da habe ich mir doch mal wieder ein paar Gedanken zu den guten alten Konzepten der Mengen gemacht und bin zu der Überzeugung gekommen, dass Mengen nicht nur durch ihre Aufzählung allein genügend charakterisiert sind. Vielmehr sollte es doch auch eine implizite Möglichkeit geben, Mengen zu beschreiben. Dies passiert eben ganz einfach durch die Verwendung von Funktionen. So lässt sich etwa die Menge {1, 2, 3} mit den Element 1, 2 und 3 ja auch durch eine Prädikatsfunktion wie folgt beschreiben.

         / tt  falls x∈{1, 2, 3}
  f x = |
         \ ff  sonst

Zunächst scheint es, als hätten wir die Aufzählung nur einfach wegabstrahiert. Jedoch kann die Aussage x∈{1, 2, 3} ebenso in eine äquivalente Form x=1 ∨ x=2 &or x=3 gebracht werden.

Schauen wir nun, was bei Negation dieser impliziten Charakterisierung passiert. Welche Menge beschreibt etwa die Funktion g x = ¬(f x)? Schauen wir einmal, welche Elemente alle darin enthalten sind.

g 1 = ¬(f 1) = ¬tt = ff
g f = ¬(f f) = ¬ff = tt
g g = ¬(f g) = ¬ff = tt

Interessanterweise enthält g also nicht nur alle natürlichen Zahlen außer der 1, 2 oder 3, sondern enthält auch alle Funktionen, insbesondere also auch f und sich selbst. Wir haben also mit g eine Menge beschrieben, die sich selbst enthält - und sich insbesondere echt enthält, also eine echte Teilmenge von sich selbst ist. Ein Widerspruch?

Sollte die Verwirrung noch nicht ausreichend sein, versuchen wir nun einmal eine Menge zu konstruieren, die sich selbst beschreibt - die also nicht nur eine (echte) Teilmenge von sich selbst ist, sondern sich selbst ist. Wir benötigen also eine Funktion, die, wenn auf sich selbst angewendet, tt als Ergebnis liefert, und ansonsten eben ff. Versuchen wir es also mit der folgenden Definition.

       / tt  falls x = h
h x = |
       \ ff  sonst

Die Funktion scheint soweit zu funktionieren, erzeugt jedoch das neue Problem, etwas über die Vergleichbarkeit zweier Funktionen aussagen zu müssen. Im strengen Sinne sind zwei Funktionen genau dann gleich, wenn sie gleiche Urbild- und Bildmengen besitzen. Es spielt also keine Rolle, in welcher Art und Weise die Mengen zueinander erzeugt werden. Lediglich die Beschreibung des Verhältnisses der beiden Mengen ist entscheidend. Nicht jedoch die Berechnungsvorschrift. So sind inbesondere die folgenden Funktionen im Sinne dieses Verständnisses alle gleich:

m1 x = x + x
m2 x = 2 * x
m3 x = (x + x + x + x) / 4

Verträgt sich dies denn auch mit unserer Definition von h? Ich würde behaupten ja. Denn wenngleich ich eine scheinbar andere Funktion als Argument von h auf h anwenden würde, liefert h bei den entsprechenden Eingaben, das intendierte Verhalten. Insbesondere folgt damit aber auch, dass h bei syntaktisch unterschiedlichen Eingaben jeweils tt liefert, die Menge jedoch trotzdem nur eine Element (eben h) enthält.

Fazit: Wir haben es also geschafft, uns von einer expliziten Mengendarstellung hin zu einer impliziten Darstellung zu bewegen und können nun etwas beschreiben, dessen Beschreibung sich selbst enthält. Ob das nur gut geht?!

Diplomarbeit angemeldet

Nach mittlerweile <censored> Semestern, durfte ich nun endlich zur Tat schreiten und meine Diplomarbeit anmelden. Der ruhmlose Titel lautet "Pläne und Spiele – eine Anwendung für spielbasiertes Model Checking". Was tatsächlich dahinter steckt, wird in spätestens sechs Monaten in jeder gut sortierten Bereichsbibliothek für Informatik in Dortmund zu lesen sein. Um es noch präziser jedem, der es nicht wissen will, vor die Stirn zu schmettern: Meine Abgabetermin wurde auf den 10.8.2006 festgesetzt. Das birgt nun natürlich den unschätzbaren Vorteil, für alles und jeden immer die geniale Ausrede parat zu haben, im Moment so wenig Zeit zu haben, weil man ja seine Diplomarbeit (die man unter uns Diplomanden auch mal ganz pfiffig mit 'DA' abkürzt) schreibt.

Also, auf geht's. Ich hab jetzt nämlich keine Zeit.

Das Halteproblem

Das Halteproblem, beschreibt die Tatsache, dass es kein Programm geben kann, das für ein anderes Programm entscheiden kann, ob dieses hält oder nicht. Endlosschleifen lassen sich für den allgemeinen Fall also nicht durch einen einfachen (oder auch komplizierten) Algorithmus ausfindig machen. Dass noch nicht einmal Namen, die man für Aufrufe verfolgen könnte, notwendig für eine Endlosschleife sind, zeigt das folgende Beispiel.

    (λ () . (λ x. (x x)) (λ x. (x x)))

Einen anschaulichen Beweis für dieses Problem habe ich heute bei Structure & Interpretation of Computer Programs wiedergefunden, den ich kurz vorführen möchte.

Angenommen, es gäbe eine Funktion safe(f, a), die für eine Funktion f und ein Argument a, herausfindet, ob f(a) definiert ist oder nicht - ob ein die Funktion f berechnendes Programm also irgendwann zu einem Ergebnis kommt, oder ewig lange in einer Endlosschleife verharrt und damit kein Resultat liefert. Formal beschreiben wir die Funktion safe wie folgt.

              / tt    falls f(a)≠⊥
safe(f, a) = |
              \ ff    sonst

Die Annahme einer solchen Funktion führt jedoch zu einem Widerspruch, wenn wir folgende Funktion betrachten.

        / ⊥    falls safe(d, d)
d(x) = |
        \ 3    sonst

Doch wozu wertet nun d(d) aus? Dies hängt von safe und insbesondere von safe(d, d) ab. Wir schauen uns die beiden Fälle einfach mal an.

safe(d, d)=true
Dann gilt d(d)=⊥. safe würde jedoch nur true liefern, wenn d(d)≠⊥ gilt. Als kann nicht gelten safe(d, d)=true.

safe(d, d)=false
Dann jedoch gilt d(d)=3. safe kann jedoch nur false liefern, wenn gilt d(d)=⊥. Es kann also auch nicht gelten safe(d, d)=false.

In beiden Fällen haben wir einen Widerspruch produziert und können daher nur annehmen, dass eine gewünschte Funktion safe mit besagten Eigenschaften nicht existieren kann. Schade.